Разделяне на кръга за произволен брой равни части
Условията на конструкции обиколка
Затворен кръг се нарича крива, всяко от които е на еднакво разстояние от точка О, наречен центъра.
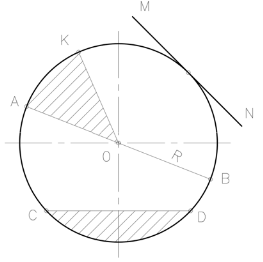
Правите линии, свързващи всяка точка на окръжността с център се нарича радиус R. Direct AB свързване на две точки на окръжността, минаваща през центъра О, наречен диаметър D. Частта на окръжността се наричат дъги. Direct CD, свързващ две точки на окръжността се нарича хорда. Директен MN, който има само една обща точка с окръжността се нарича допирателна. Част от кръг, ограничена от акорд и дъга CD се нарича sigmente. Част от кръг, ограничена от два радиуса и дъга се нарича сектор. Два взаимно perpindikulyarnye хоризонтални и вертикални линии, пресичащи се в центъра на кръга, наречени оста на кръга. Ъгълът, образуван от две радиуси КОА се нарича централен ъгъл. Две взаимно перпендикулярни радиус 90 образуват ъгъл от 0 и 1/4 кръг граница.
Разделяне периферно 4-D и 8-НИЛ идентични части
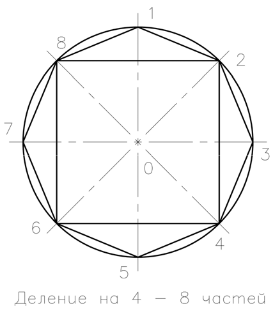
Направи кръг с хоризонтални и вертикални оси, които го разделят на 4 равни части в D. Извършва с шублер или от 450 гон, две перпендикулярни линии разделят окръжността на 8 равни части нула.
Разделяне на окръжността, 3 и 6 равни части (три кратни на 3)
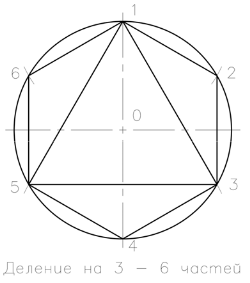
За да се разделят на обиколката на 3,6 пъти и ги носи на броя на части и обиколката на предварително определен радиус, съответстващ ос. Разделянето може да започне от точката на пресичане на хоризонтална или вертикална ос, с обиколката. Предварително определената радиуса на последователно кръг забавено 6-пет пъти. След това, тези точки върху кръга последователно свързан с прави линии, за да образуват истински тест шест многоъгълник с надпис. Свързване точки чрез един дава равностранен триъгълник, и се разделят на обиколката на три равни части.
Разделяне на кръга в 5 и 10 е пет равни части
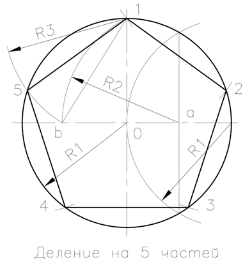
Изграждане на равностранен петоъгълник, както следва. Равен две взаимно перпендикулярни оси обиколката, равен на диаметъра на кръга. Разделете дясната половина на половината от хоризонтален диаметър през дъга от R1. От получения точка "а" в средата на този интервал от радиус R2 провеждане на дъга от окръжност до неговото пресичане с хоризонталната диаметър в точка "В". Радиус R3 от точка "1" се извършва до пресичането на кръгова дъга с предварително окръжност (V.5) дава посока на обикновен петоъгълник. Разстоянието "б-On" дава правилната страна на десетоъгълник.
Разделяне периферно N-Noe брой идентични единици (изграждането на правилен многоъгълник на N страни)
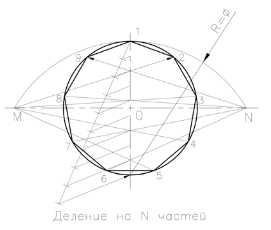
Това е, както следва. Обръщаме на хоризонталните и вертикалните оси са взаимно перпендикулярни обиколка. От горната точка "1" кръг провеждане на произволна ъгъл спрямо вертикалната ос на права линия. Това отлагане на равни сегменти на произволна дължина, равен на броя на частите, към която разделя тази окръжност, например 9. В края на последния сегмент, свързан към долната точка на вертикалната диаметър. Равен линии, успоредни, получени от всички висящи сегменти до пресечната точка с вертикална диаметър, като по този начин се раздели вертикално диаметъра на кръга от предварително определен брой части. Радиус равен на диаметъра на окръжността на долната точка на вертикалната ос на стопанство дъга Мп до неговото пресичане с хоризонталната разширението на оста на кръга. От точките М и N провеждане греди през вечерта (или нечетните) на точката разделяне на вертикален диаметър на кръга на пресичане. Ще се търсят Получените кръгови сегменти, тъй точки 1, 2, .... 9 разделят на кръга в 9-Th (N) равни части.
Намирането на центъра на дъгата
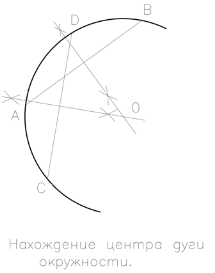
За да намерите центъра на обиколката на дъга postraeniya извърши следното: за бележка дадена дъга четири произволни точки A, B, C, D и да ги комбинирате по двойки струни AB и CD. Всяка от хордите с компас на две половини, като по този начин перпендикулярно, минаваща през центъра на съответния хордата. Припокриването на тези вертикалите дава центъра на дъгата и съответния кръг.