Какви са нули и това е интервалите на функция постоянен знак studopediya

Помислете функция.

1) точките, в които графиката пресича оста. наречени нули. За да намерите най-нули на функцията е необходимо да се реши уравнението. тоест, да намерите на стойностите на "Х". при които функцията изчезва. Следните хипотетичен пример функция нули са обозначени с червени точки:

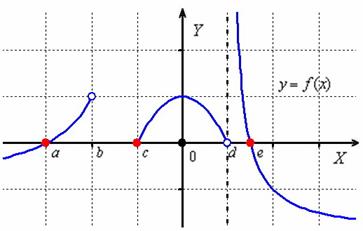
Очевидно е, че. Имайте предвид, че точката не е функцията нула, тъй като тя не е част от областта на дефиниция.

2) Интервалът на постоянен знак - е интервала от време, в които всяка точка е положителна или отрицателна.

В нашия случай, ние сме позитивно върху интервала. това е, за всяка стойност на "X" на някое от горните интервали строго неравенство. Или просто - графика на функцията на интервали са разположени над оста х.

На интервали функция е отрицателно, т.е. всяка стойност "X", принадлежащи към тези интервали съответства на строг неравенството. и функция график се намира под оста.

Компактен запис на тези факти е, както следва:
. ако;
. ако.
Strings може да се преобразува в някои места, това няма значение, аз лично използва за обозначаване на интервали в началото, което е положително.

Какво може да се каже и за границите. Само че не е определено в този интервал, и, разбира се, за постоянството на знак на словото не излиза изобщо.

Забележка. в математиката е по-широка Терминът "пролука", която включва не само интервала, но интервала или сегмент. Интервали и интервали от постоянен знак често се срещат ukusochno определени функции. По-специално, ако в горната фигура, "боя" точката с абсциса, получаваме интервала (в този случай - интервал) на постоянен знак. Но ще продължим да се счита за "нормални" функции само с интервали от постоянен знак, така че понятието "период на постоянен знак" не специални нужди.