уравнение модул

Геометричната интерпретация на модула: това е разстоянието от точка 0 до точка по ос координира.

Да - алгебричен израз. След това, използвайки дефиницията на модул (9) под съответните предположения, ние може да разкрие знака на абсолютната стойност на израза:

Уравнението съдържащ неизвестно експресия х под знака модул, наречен уравнението на модула.

Помислете за основните видове уравнения с модула и методите за тяхното разрешаване.

Нека нататък. , - някои изрази с променлива х. и.

където - брой, - израз на неизвестно х.

1. Ако. Уравнение (10) няма разтвор.

2. Ако. Уравнение (10) е еквивалентна на уравнението.

3. Ако. Уравнение (10) набор от уравнения е еквивалентен на:

къде. - някои от изразите на неизвестно х.

За да реши това уравнение по няколко начина.

Първата способност използване определение модул:

Второ способност с помощта на подхода към решаването на това как да се уравнения от тип I с допълнително условие за знака на израза:

Забележка: 1-ви или 2-ри начин на решаване на тези уравнения са избрани в зависимост от това коя от неравенството или решен лесно.

Третият метод способни интервали. трябва да:

1) Намерете стойностите на х. за които

2) Нанесете получените стойности на х в реално ос;

3) определяне на признаците за всеки от получените ленти;

4) изготвя крива марка;

5) за решаване на уравнението за всеки интервал индивидуално, разкрива модул съгласно фигура;

6) за всеки специфичен интервал да се провери дали или не са получени корени принадлежат към този интервал;

7) в отговора за обозначаване на съвкупността от всички получени корени.

Тип III: уравнения, съдържащи няколко модула. Ако двамата, след това уравнение е от вида:

къде. , , - някои от изразите на неизвестно х.

1-ви начин - можете да използвате определението за модул и счита 4 случаи на възможни признаци. , Този метод, като правило, не е рационално.

Метод 2 -Метод интервали. Необходимо е да се направи най-много числени оси и криви признаци като модули в уравнението. За уравнение (11) изготвя двете оси, поставянето им една под друга (една ос за втората -. До). За всеки израз и да изобразяват кривата на оценките на съответната ос. След това отворете модулите с помощта на снимката и решаване на уравнението отделно на всеки интервал. Подходящи само тези корени, които принадлежат на разглеждания период. В отговор, трябва да посочите набор от получените корени.

Първият метод - разтвор на уравнение (12) се редуцира до решаване на набор от уравнения:

2-ри метод способност интервали (не рационално).

Трети метод - след изграждането на уравнението в квадрата и използването на свойствата на модула се редуцира до уравнението е еквивалентен на:

Получената уравнение се решава в зависимост от неговия вид.

Тип V: уравнение решен заместител променлива, например

До имота на модула е написана под формата

Приложен подмяна и решаване на квадратно уравнение, получено в неизвестното. Тогава ще трябва да се върнем към старата променлива. В случай на 2 различни корените на квадратното уравнение е набор от уравнения е тип I:

ако коренът е единственият, който остава да се реши уравнението

Трябва да се помни, че в случай на уравнение с отрицателна стойност на модула още няма решения.

Това уравнение пиша. Неговата TCC :.

Уравнението може да се запише като

. На ДХС може да бъде намалена и получаваме

подходяща за DHS.

Пример 2: решаване на уравнение.

Това уравнение II тип. Неговата TCC :. Той има решение, ако. т.е. в. По този начин, за да се получи

Ние решаваме получили отделно дробни рационални уравнения. Първият уравнението намалява да имат

Това е квадратно уравнение няма решение, защото ,

От втория уравнение набор от (13) получаваме

В квадратно уравнение има корени:

Въпреки това, т.е. първият корен не принадлежи. който решава уравнението отговор е само.

Тип II има уравнение, което ще вземе решение за определянето на модула.

Решаването на системата от първото множество (14):

Стойността не е подходящо за състоянието. Остава корен.

Решаването на системата от второто множество (14):

Пример 4. решаване на уравнение.

Тъй като. то уравнението може да се запише като

Това уравнение се отнася до тип III уравнения.

Неговата TCC :. Ние решаваме метода на интервали от време.

Нули на експресията при модул са:

Тези числени стойности са разделени на три ос пространство.

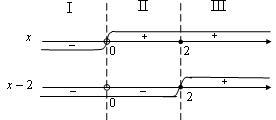
Разширяване на елемента на всяка от получените пропуски, като се вземат предвид техните марки, се определя на системи за:

Ние решаваме системата отделно.